pyanno Package

pyanno Package

• models Module
  • modelB Module
  • modelBt Module
  • modelBt_loopdesign Module
  • modelA Module
• annotations Module
  • annotations Module
• measures Package
  • measures Package
  • agreement Module
  • covariation Module
  • distances Module
  • helpers Module
• database Module
  • database Module
• plots Package
  • plots Package

Other modules

abstract_model Module

Defines AbstractModel, an abstract class that specifies the interface of pyAnno models.

class pyanno.abstract_model.AbstractModel

Bases: traits.has_traits.HasTraits

Abstract class defining the interface of a pyAnno model.

are_annotations_compatible(annotations)

Returns True if the annotations are compatible with the model.

The standard implementation is: valid if the number of annotators is correct, if the classes are between 0 and nclasses-1, and if missing values are marked with pyanno.util.MISSING_VALUE

static create_initial_state(nclasses)

Factory method returning a model with random initial parameters.

Parameters:nclasses (int) – Number of label classes

generate_annotations(nitems)

Generate a random annotation set from the model.

Sample a random set of annotations from the probability distribution defined the current model parameters.

Parameters:nitems (int) – Number of items to sample Returns:annotations (ndarray, shape = (n_items, n_annotators)) - annotations[i,j] is the annotation of annotator j for item i

infer_labels(annotations)

Infer posterior distribution over label classes.

Compute the posterior distribution over label classes given observed annotations, .

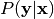annotations : ndarray, shape = (n_items, n_annotators)

annotations[i,j] is the annotation of annotator j for item i

Returns:posterior (ndarray, shape = (n_items, n_classes)) - posterior[i,k] is the posterior probability of class k given the annotation observed in item i.

log_likelihood(annotations)

Compute the log likelihood of a set of annotations given the model.

Returns log P(annotations | current model parameters).

Parameters:annotations (ndarray, shape = (n_items, n_annotators)) – annotations[i,j] is the annotation of annotator j for item i Returns:log_lhood (float) - log likelihood of annotations

map(annotations)

Computes maximum a posteriori (MAP) estimate of parameters.

Estimate the model parameters from a set of observed annotations using maximum a posteriori estimation.

Parameters:annotations (ndarray, shape = (n_items, n_annotators)) – annotations[i,j] is the annotation of annotator j for item i

mle(annotations)

Computes maximum likelihood estimate (MLE) of parameters.

Estimate the model parameters from a set of observed annotations using maximum likelihood estimation.

Parameters:annotations (ndarray, shape = (n_items, n_annotators)) – annotations[i,j] is the annotation of annotator j for item i

sample_posterior_over_accuracy(annotations, nsamples, burn_in_samples=0, thin_samples=1)

Return samples from posterior over the accuracy parameters.

Draw samples from P(accuracy parameters | data, model parameters). The accuracy parameters control the probability of an annotator reporting the correct label (the exact nature of these parameters varies from model to model).

Parameters:

• annotations (ndarray, shape = (n_items, n_annotators)) – annotations[i,j] is the annotation of annotator j for item i
• nsamples (int) – Number of samples to return (i.e., burn-in and thinning samples are not included)
• burn_in_samples (int) – Discard the first burn_in_samples during the initial burn-in phase, where the Monte Carlo chain converges to the posterior
• thin_samples (int) – Only return one every thin_samples samples in order to reduce the auto-correlation in the sampling chain. This is called “thinning” in MCMC parlance.

Returns:

samples (ndarray, shape = (n_samples, ??)) - Array of samples from the posterior distribution over parameters.

util Module

Utility functions.

exception pyanno.util.PyannoValueError

Bases: exceptions.ValueError

ValueError subclass raised by pyAnno functions and methods.

class pyanno.util.benchmark(name)

Bases: object

Simple context manager to simplify benchmarking.

Usage:

with benchmark('fast computation'):
    do_something()

pyanno.util.compute_counts(annotations, nclasses)

Transform annotation data in counts format.

At the moment, it is hard coded for 8 annotators, 3 annotators active at any time.

Parameters:

• annotations (ndarray, shape = (n_items, 8)) – Annotations array
• nclasses (int) – Numer of label classes

Returns:

data (ndarray, shape = (n_classes^3, 9)) - data[i,m] is the number of times the combination of annotators number m voted according to pattern i

pyanno.util.create_band_matrix(shape, diagonal_elements)

Create a symmetrical band matrix from a list of elements.

Parameters:

• shape (int) – Width of the matrix
• diagonal_elements (list or array) – List of elements in the first row. If the list is smaller than shape, the last element is used to fill the the remaining items.

pyanno.util.dirichlet_llhood(theta, alpha)

Compute the log likelihood of theta under Dirichlet(alpha).

Parameters:

• theta (ndarray) – Categorical probability distribution. theta[i] is the probability of item i. Elements of the array have to sum to 1.0 (not forced for efficiency reasons)
• alpha (ndarray) – Parameters of the Dirichlet distribution

Returns:

log_likelihood (float) - Log lihelihood of theta given alpha

pyanno.util.is_valid(annotations)

Return True if annotation is valid.

An annotation is valid if it is not equal to the missing value, MISSING_VALUE.

pyanno.util.labels_count(annotations, nclasses, missing_val=-1)

Compute the total count of labels in observed annotations.

Parameters:

• annotations (ndarray, shape = (n_items, n_annotators)) – annotations[i,j] is the annotation made by annotator j on item i
• nclasses (int) – Number of label classes in annotations
• missing_val (int) – Value used to indicate missing values in the annotations. Default is MISSING_VALUE

Returns:

count (ndarray, shape = (n_classes, )) - count[k] is the number of elements of class k in annotations

pyanno.util.labels_frequency(annotations, nclasses, missing_val=-1)

Compute the total frequency of labels in observed annotations.

Parameters:

• annotations (ndarray, shape = (n_items, n_annotators)) – annotations[i,j] is the annotation made by annotator j on item i
• nclasses (int) – Number of label classes in annotations
• missing_val (int) – Value used to indicate missing values in the annotations. Default is MISSING_VALUE

Returns:

freq (ndarray, shape = (n_classes, )) - freq[k] is the frequency of elements of class k in annotations, i.e. their count over the number of total of observed (non-missing) elements

pyanno.util.majority_vote(annotations)

Compute an estimate of the real class by majority vote.

In case of ties, return the class with smallest number.

Parameters:annotations (ndarray, shape = (n_items, n_annotators)) – annotations[i,j] is the annotation made by annotator j on item i

vote : ndarray, shape = (n_items, )

vote[i] is the majority vote estimate for item i

pyanno.util.ninf_to_num(x)

Substitute -inf with smallest floating point number.

pyanno.util.normalize(x, dtype=<type 'float'>)

Returns a normalized distribution (sums to 1.0).

If x consists only of zero element, the returned array has elements 1/n , where n is the length of x.

pyanno.util.random_categorical(distr, nsamples)

Return an array of samples from a categorical distribution.

Parameters:

• distr (ndarray) – distr[i] is the probability of item i
• nsamples (int) – Number of samples to draw from the distribution

Returns:

samples (ndarray, shape = (n_samples, )) - Samples from the distribution

pyanno.util.string_wrap(st, mode)

pyanno.util.MISSING_VALUE = -1

In annotations arrays, this is the value used to indicate missing values

pyanno.util.SMALLEST_FLOAT = -1.7976931348623157e+308

Smallest possible floating point number, somtimes used instead of -np.inf to make numberical calculation return a meaningful value

sampling Module

This module defines functions to sample from a distribution given its log likelihood.

pyanno.sampling.optimize_step_size(likelihood, x0, arguments, x_lower, x_upper, n_samples, recomputing_cycle, target_rejection_rate, tolerance)

Compute optimum jump for MCMC estimation of credible intervals.

Adjust jump size in Metropolis-Hasting MC to achieve target rejection rate. Jump size is estimated for each parameter separately.

Parameters:

• likelihood (function(params, arguments)) – Function returning the unnormalized log likelihood of data given the parameters. The function accepts two arguments: params is the vector of parameters; arguments contains any additional argument that is needed to compute the log likelihood.
• x0 (ndarray, shape = (n_parameters, )) – Initial parameters value.
• arguments (any) – Additional argument passed to the function likelihood.
• x_lower (ndarray, shape = (n_parameters, )) – Lower bound for the parameters.
• x_upper (ndarray, shape = (n_parameters, )) – Upper bound for the parameters.
• n_samples (int) – Total number of samples to draw during the optimization.
• recomputing_cycle (int) – Number of samples over which the rejection rates are computed. After recomputing_cycle samples, the step size is adapted and the rejection rates are reset to 0.
• target_rejection_rate (float) – Target rejection rate. If the rejection rate over the latest cycle is closer than tolerance to this target, the optimization phase is concluded.
• tolerance (float) – Tolerated deviation from target_rejection_rate.

Returns:

step (ndarray, shape = (n_parameters, )) - The final optimized step size.

pyanno.sampling.sample_distribution(likelihood, x0, arguments, step, nsamples, x_lower, x_upper)

General-purpose sampling routine for MCMC sampling.

Draw samples from a distribution given its unnormalized log likelihood using the Metropolis-Hasting Monte Carlo algorithm.

It is recommended to optimize the step size, step, using the function optimize_step_size() in order to reduce the autocorrelation between successive samples.

Parameters:

• likelihood (function(params, arguments)) – Function returning the unnormalized log likelihood of data given the parameters. The function accepts two arguments: params is the vector of parameters; arguments contains any additional argument that is needed to compute the log likelihood.
• x0 (ndarray, shape = (n_parameters, )) – Initial parameters value.
• arguments (any) – Additional argument passed to the function likelihood.
• step (ndarray, shape = (n_parameters, )) – Width of the proposal distribution over the parameters.
• nsamples (int) – Number of samples to draw from the distribution.
• x_lower (ndarray, shape = (n_parameters, )) – Lower bound for the parameters.
• x_upper (ndarray, shape = (n_parameters, )) – Upper bound for the parameters.

pyanno.sampling.sample_from_proposal_distribution(theta, step, lower, upper)

Returns one sample from the proposal distribution.

Parameters:

• theta (float) – current parameter value
• step (float) – width of the proposal distribution over theta
• lower (float) – lower bound for theta
• upper (float) – upper bound for theta

Returns:

• theta_new (float) - new sample from the distribution over theta
• log_q_ratio (float) - log-ratio of probability of new value given old value to probability of old value given new value