quantlib.models.shortrate.onefactormodels.hullwhite.

HullWhite

class HullWhite(HandleYieldTermStructure term_structure, Real a=0.1, Real sigma=0.01)

Bases: Vasicek

Single-factor Hull-White (extended Vasicek) model.

The standard single-factor Hull-White model is defined by

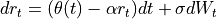
dr_t = (\theta(t) - \alpha r_t)dt + \sigma dW_t

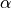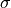where \alpha and \sigma are constants.

Warning

When the term structure is relinked the 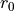r_0 parameter of the underlying Vasicek model is not updated.

Attributes:
Lambda
a
b
dynamics

short-rate dynamics

r0
sigma

Methods

calibrate(self, list helpers, ...)

convexity_bias(Real future_price, Time t, ...)

Futures convexity bias

discount_bond(self, Time now, Time maturity, ...)

discount_bond_option(self, ...)

params(self)

set_params(self, Array params)