Blocks

Creating a Block object is as simple as invoking it on a string containing some Python code:

>>> from codetools.blocks.api import Block
>>>
>>> b = Block("""# my calculations
... velocity = distance/time
... momentum = mass*velocity
... """)

The code in the Block can be executed by using its execute() method in much the same way that the exec() statement works:

>>> global_namespace = {}
>>> local_namespace = {'distance': 10.0, 'time': 2.5, 'mass': 3.0}
>>> b.execute(local_namespace, global_namespace)

After this code, the variables local_namespace and global_namespace hold the same contents as if the Block’s code had been executed by the exec() statement. In particular:

>>> local_namespace
{'distance': 10.0, 'mass': 3.0, 'time': 2.5, 'velocity': 4.0, 'momentum': 12.0}

Whenever you create a Block, it performs an analysis of the code, so the block can tell you which variables are its inputs and outputs:

>>> b.inputs
set(['distance', 'mass', 'time'])
>>> b.outputs
set(['velocity', 'momentum'])

In more complex situations, the Block object can give further useful information about the code, such as imported names and variables which may conditionally be output.

Restricting Execution

Where the Block object is unique is that it is aware of which variables are dependent on which other variables within its code. This allows you to restrict the code that is executed by specifying which input and output variables you are concerned with. This is achieved through the restrict() method of the Block object, which expects one or both of the following arguments:

inputs

a list or tuple of input variables

outputs

a list or tuple of output variables

For example:

>>> restricted_block = b.restrict(inputs=('mass',))

This restricted block consists of every line that depends on the variable mass in the original code block. In this case, this is the single line:

momentum = mass*velocity

Internally, the Block object maintains a representation of the code block as an abstract syntax tree from the Python standard library compiler package. This representation is not particularly human-friendly, but the unparse() function allows us to reconstruct the Python source:

>>> restricted_block.ast
Assign([AssName('momentum', 'OP_ASSIGN')], Mul((Name('mass'), Name('velocity'))))
>>> from codetools.blocks.api import unparse
>>> unparse(restricted_block.ast)
'momentum = mass*velocity'

This allows us to perform the minimum amount of recalculation in response to changes in the inputs. For example, if we change mass in the local name space, then we only need to execute the restricted block which depends upon mass as input:

>>> local_namespace['mass'] = 4.0
>>> restricted_block.execute(local_namespace, global_namespace)
>>> local_namespace
{'distance': 10.0, 'mass': 3.0, 'time': 2.5, 'velocity': 4.0, 'momentum': 16.0}

On the other hand, if we are interested in calculating only a particular output, we can restrict on the outputs:

>>> velocity_comp = b.restrict(outpts=('velocity',))
>>> unparse(velocity_comp.ast)
'velocity = distance/time\n'
>>> velocity_comp.inputs
set(['distance', 'time'])

Note

Block restriction is designed to answer the questions “What do I need to compute when this changes?” or “What do I need to compute to calculate this output?” It doesn’t (yet) answer the question “If I have these inputs, what outputs can I calculate?”

Example: Rocket Science

At this point, an extended example is probably worthwhile. Consider the following code which calculates quantities involved in the motion of a rocket as it loses reaction mass:

from helper import simple_integral

thrust = fuel_density*fuel_burn_rate*exhaust_velocity + nozzle_pressure*nozzle_area

mass = mass_rocket + fuel_density*(fuel_volume - simple_integral(fuel_burn_rate,t))

acceleration = thrust/mass

velocity = simple_integral(acceleration, t)

momentum = mass*velocity

displacement = simple_integral(velocity, t)

kinetic_energy = 0.5*mass*velocity**2

work = simple_integral(thrust, displacement)

The simple_integral() function in the helper module looks something like this:

from numpy import array, ones

def simple_integral(y, x):
    """Return an array of trapezoid sums of y"""
    dx = x[1:] - x[:-1]
    if array(y).shape == ():
        y_avg = y*ones(len(dx))
    else:
        y_avg = (y[1:]+y[:-1])/2.0
    integral = [0]
    for i in xrange(len(dx)):
      integral.append(integral[-1] + y_avg[i]*dx[i])
    return array(integral)

Inputs to these computations are expected to be either scalars or 1-D Numpy arrays that hold the values of quantities as they vary over time. Some of these computations, particularly the simple_integral() computations, are potentially expensive. We can set up a Block to hold this computation:

>>> rocket_science = """
...    ...
... """
>>> rocket_block = Block(rocket_science)
>>> rocket_block.inputs
set(['fuel_volume', 'nozzle_area', 'fuel_density', 'nozzle_pressure', 'mass_rocket',
'exhaust_velocity', 'fuel_burn_rate', 't'])
>>>
>>> rocket_block.outputs
set(['acceleration', 'work', 'mass', 'displacement', 'thrust', 'velocity',
'kinetic_energy', 'momentum'])

We can use this code by setting up a dictionary of local values for the inputs and then inspecting it:

>>> from numpy import linspace
>>> local_namespace = dict(
...     mass_rocket = 100.0,         # kg
...     fuel_density = 1000.0,       # kg/m**3
...     fuel_volume = 0.060,         # m**3
...     fuel_burn_rate = 0.030,      # m**3/s
...     exhaust_velocity = 3100.0,   # m/s
...     nozzle_pressure = 5000.0,    # Pa
...     nozzle_area = 0.7,           # m**2
...     t = linspace(0.0, 2.0, 2000) # calculate every millisecond
... )
>>> rocket_block.execute(local_namespace)
>>> print local_namespace["velocity"][::100]  # values every 0.1 seconds
[    0.            60.91584683   123.00759628   186.32154205   250.90676661
   316.81536979   384.10272129   452.82774018   523.05320489   594.84609779
   668.27798918   743.42546606   820.37061225   899.2015473    980.01303322
  1062.90715923  1147.9941173   1235.39308291  1325.23321898  1417.65482395]
>>>
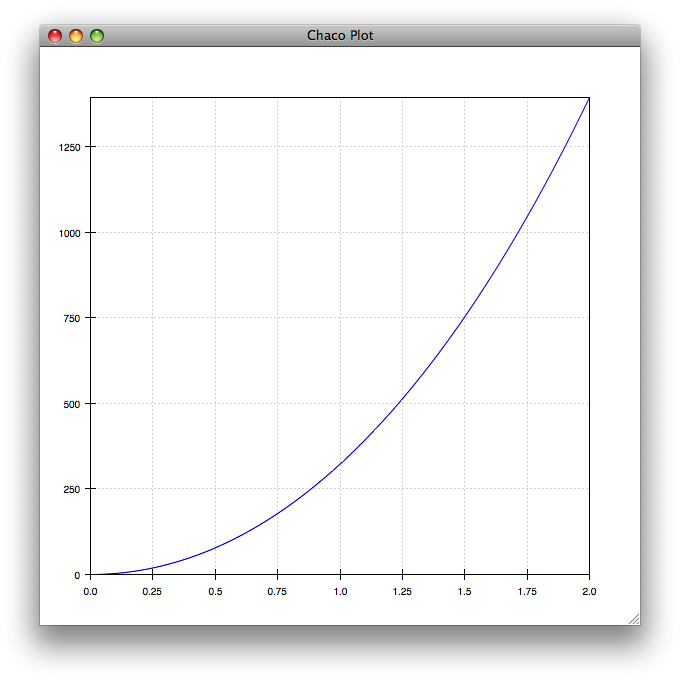
>>> from chaco.shell import *
>>> plot(local_namespace['t'], local_namespace["displacement"], "b-")
>>> show()

Restricting on Inputs

If we want to change the inputs into this calculation, say to increase the nozzle area of the rocket to 0.8 m**2 and decrease the nozzle pressure to 4800 Pa, then we don’t want to have to recalculate everything. We want to calculate only the quantities which depend upon nozzle_pressure and nozzle_area. We can do this as follows:

>>> restricted_block = rocket_block.restrict(inputs=("nozzle_area", "nozzle_pressure"))
>>> local_namespace["nozzle_area"] = 0.8
>>> local_namespace["nozzle_pressure"] = 4800
>>> restricted_block.execute(local_namespace)
>>> print local_namespace["velocity"][::100]
[    0.            61.13047262   123.44099092   186.97801173   251.79079045
   317.93161047   385.45603658   454.42319544   524.89608665   596.9419286
   670.63254375   746.04478895   823.2610372    902.36971856   983.46592888
  1066.65211709  1152.03886341  1239.7457632   1329.90243447  1422.64966996]
>>> print local_namespace["displacement"][::100]
[    0.             3.04840167    12.27156425    27.78985293    49.72841906
    78.21749145   113.39269184   155.39537691   204.37300999   260.47956554
   323.87597012   394.73058422   473.21972951   559.52826736   653.8502346
   756.38954417   867.36075888   986.98994825  1115.51563971  1253.18987771]

Other values from the namespace can be extracted similarly.

The structure of the new block can be observed from its traits:

>>> restricted_block.outputs
set(['acceleration', 'work', 'displacement', 'thrust', 'velocity', 'kinetic_energy',
'momentum'])
>>> print unparse(restricted_block.ast)
from numpy import array, sum, ones, linspace
thrust = fuel_density*fuel_burn_rate*exhaust_velocity+nozzle_pressure*nozzle_area
acceleration = thrust/mass
velocity = simple_integral(acceleration, t)
kinetic_energy = 0.5*mass*velocity**2
displacement = simple_integral(velocity, t)
momentum = mass*velocity
work = simple_integral(thrust, displacement)

Restricting on Outputs

In the plot above, we only really needed to know the value of displacement — so to simplify the calculation of that value for the plot, we could have restricted on the output:

>>> restricted_block = rocket_block.restrict(outputs=("displacement",))
>>> local_namespace["mass_rocket"] = 110
>>> restricted_block.execute(local_namespace)

Once again, we can introspect the code block and have a look at what is actually going on:

>>> restricted_block.inputs
set(['fuel_volume', 'nozzle_area', 'fuel_density', 'nozzle_pressure',
'exhaust_velocity', 'mass_rocket', 't', 'fuel_burn_rate'])
>>> unparse(restricted_block.ast)
thrust = fuel_density*fuel_burn_rate*exhaust_velocity + nozzle_pressure*nozzle_area
mass = mass_rocket + fuel_density*(fuel_volume - simple_integral(fuel_burn_rate,t))
acceleration = thrust/mass
velocity = simple_integral(acceleration, t)
displacement = simple_integral(velocity, t)

Restricting on Both

If we wanted to go even further, and just update the plot depending on changes to just one of the inputs (say, mass_rocket), we could do the following:

>>> restricted_block = rocket_block.restrict(inputs=("mass_rocket",),
...     outputs=("displacement",))
>>> unparse(restricted_block.ast)
mass = mass_rocket + fuel_density*(fuel_volume - simple_integral(fuel_burn_rate,t))
acceleration = thrust/mass
velocity = simple_integral(acceleration, t)
displacement = simple_integral(velocity, t)

To really see the full power of the Block class, and to incorporate it into programs, we really need the other half of the system: the DataContext class.